
Môn Toán
Giải phương trình, bất phương trình bằng cách sử dụng tính đơn điệu của hàm số
- Kiến thức cơ bản
-
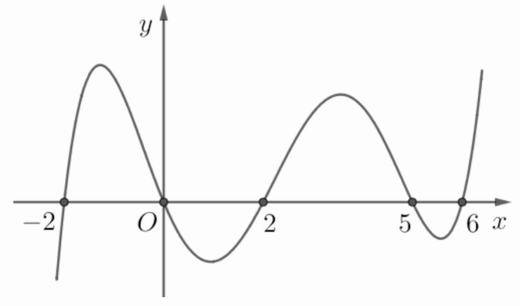
- Định lí 1. Nếu hàm số f(x) luôn luôn đồng biến hoặc luông luôn nghịch biến và liên tục trên tập xác định D thì số nghiệm của phương trình f(x) = a trên tập xác định D không quá 1 nghiệm và với mọi u, v thuộc tập D ta có f(u) = f(v) khi và chỉ khi u = v.
- Định lí 2. Nếu hàm số f(x) và g(x) đơn điệu ngược chiều và lien tục trên tập xác định D thì số nghiệm của phương trình f(x) = g(x) trên tập D không nhiều hơn 1 nghiệm.
- Định lí 3. Cho hàm số f(x) luôn đồng biến trên tập xác định D thì ta có f(x) > f(a) khi và chỉ khi x > a với x, a thuộc tập xác định D. Nếu f(x) luôn nghịch biến trên D thì ta có f(x) > f(a) khi và chỉ khi x < a với x, a thuộc tập xác định D.
- Định lí 1. Nếu hàm số f(x) luôn luôn đồng biến hoặc luông luôn nghịch biến và liên tục trên tập xác định D thì số nghiệm của phương trình f(x) = a trên tập xác định D không quá 1 nghiệm và với mọi u, v thuộc tập D ta có f(u) = f(v) khi và chỉ khi u = v.
- Định lí 2. Nếu hàm số f(x) và g(x) đơn điệu ngược chiều và lien tục trên tập xác định D thì số nghiệm của phương trình f(x) = g(x) trên tập D không nhiều hơn 1 nghiệm.
- Định lí 3. Cho hàm số f(x) luôn đồng biến trên tập xác định D thì ta có f(x) > f(a) khi và chỉ khi x > a với x, a thuộc tập xác định D. Nếu f(x) luôn nghịch biến trên D thì ta có f(x) > f(a) khi và chỉ khi x < a với x, a thuộc tập xác định D.
Đọc thêm: Giải phương trình, bất phương trình bằng cách sử dụng tính đơn điệu của hàm số
Gia sư dạy kèm tphcm chia sẻ bài toán tìm tham số m
Gia sư dạy kèm tphcm có thể nói, khi bạn luyện đến bài toán tìm tham số m để bất phương trình có nghiệm tức bạn đã có một đẳng cấp khá cao trong giải toán rồi đấy. Vì nếu bài toán này có mặt trong kì thi trung học phổ thông quốc gia thì nó nằm ở câu để lấy được 9 điểm. Quả không phải là chuyện đơn giản đúng không nào. Vì thế, mức độ khó cũng như độ phức tạp của câu này là khá cao, đòi hỏi người giải toán có nhận thức sâu và tư duy logic.

Sau đây, gia sư tphcm có một ví dụ rất hay về bài toán tham số m để bất phương trình có nghiệm, trung tâm gia sư tphcm và các bạn hãy cùng nhân phân tích và giải quyết bài toán này nhé.
Đọc thêm: Gia sư dạy kèm tphcm chia sẻ bài toán tìm tham số m
Gia sư sinh viên tphcm giải phương trình bằng phương pháp đặt ẩn phụ không triệt để
Gia sư sinh viên tphcm nhận thấy một bài toán có rất nhiều cách giải để cho ra một kết quả đúng là sự thú vị nhất trong toán học. Trong một cuộc thi toán quốc tế, có thí sinh nọ trong suốt quá trình thi của anh ta, anh ta chỉ giải đúng 1 câu nhưng có tới 13 cách giải hoàn toàn khác nhau.
Và thế là anh bạn đó đã rớt giải nhất nhì ba và khuyến khích trong cuộc thi nhưng lại nhận được giải đặc biệt vì quá thông minh.
Đọc thêm: Gia sư sinh viên tphcm giải phương trình bằng phương pháp đặt ẩn phụ không triệt để
Gia sư tại quận 4 nêu cách đặt ẩn phụ giải phương trình và bất phương trình
Gia sư tại quận 4 thấy rằng phương trình, bất phương trình là một trong những bài toán khó của môn toán và vị trí của nó là câu 9 điểm trong bài thi trung học phổ thông quốc gia. Câu phương trình, bất phương trình này khó bởi vì kiến thức rất rộng và rất sâu.

Kiến thức rộng biểu hiện ở chỗ có rất nhiều dạng để giải phương trình như cộng đại số, thêm bớt, nhân liên hợp, đặt ẩn phụ, đặt ẩn không triệt để, dùng hàm số, dùng bất đẳng thức,… và quá trình trau dồi kiến thức cho câu này là từ chương trình từ cấp 2 lên tới cấp 3.
Đọc thêm: Gia sư tại quận 4 nêu cách đặt ẩn phụ giải phương trình và bất phương trình
Trung tâm gia sư quận Thủ Đức giới thiệu một số bài toán về bất phương trình mũ – logarit
Hôm nay, Trung tâm gia sư quận Thủ Đức sẽ giới thiệu đến các bạn một số bài toán về bất phương trình mũ – logarit.

Trước tiên, trung tâm gia sư quận Tân Phú muốn các bạn nhận biết đúng đắn của bài toán bất phương trình mũ – logarit này về ứng dụng thực tiễn để có định hướng tốt cho việc học cũng như ôn luyện cho kì thi trung học phổ thông sắp tới của mình.
Đọc thêm: Trung tâm gia sư quận Thủ Đức giới thiệu một số bài toán về bất phương trình mũ – logarit
- Cảm Nhận Bài Thơ Mùa Xuân Nho Nhỏ | Gia Sư Giỏi TPHCM
- Phân tích truyện ngắn lặng lẽ sa pa hay nhất | Gia sư uy tín ở TPHCM
- Cảm Nhận Bài Thơ Tiểu Đội Xe Không Kính | Tìm gia sư uy tín ở TPHCM
- Cảm nhận của em về bài thơ Đồng Chí | Gia sư uy tín TPHCM
- Gia sư tphcm tổng hợp 3 cách phòng tránh bệnh viêm phổi vũ hán hiệu quả nhất






 0908 64 0203
0908 64 0203
