
Môn Toán
Gia sư uy tín tại tphcm nói về cộng, trừ, nhân, chia số phức
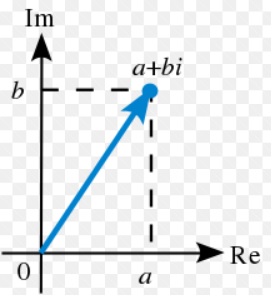
Gia sư uy tín tại tphcm cho rằng số phức là số có dạng z = a + bi, trong đó a, b là hai số thực, i là đơn vị ảo với i2 = -1, a còn được gọi là phần thực, là gọi là phần ảo. Nếu số phức đã cho có phần thực bằng 0 ( tức b = 0 ) thì số phức được gọi là số thuần ảo, nếu số phức có phần ảo bằng 0 ( tức b = 0 ) thì được gọi là số thuần thực. Một số phức hoàn toàn có thể xác định được khi được biểu diễn trên mặt phẳng phức với trục hoành là trục thực và trục tung là trục ảo.

Số phức không đơn giản chỉ có thể được sử dụng trong toán học, nó còn được áp dụng trong nhiều lĩnh vực khác như khoa học kĩ thuật, diện tử học, cơ học điện tử, toán học ứng dụng ví dụ như lý thuyết hỗn độn. Nhà toán học người Ý G.Cadano là người đầu tiên đề cặp đến số phức trong thế kỉ XVI và áp dụng nó để giải phương trình bậc 3.
Đọc thêm: Gia sư uy tín tại tphcm nói về cộng, trừ, nhân, chia số phức
Gia sư uy tín ở tphcm nói về sự ra đời của số phức
Gia sư uy tín ở tphcm thấy rằng sự ra đời của số phức đã đánh dấu một bước phát triển của toán học cũng như tư duy logic của con người. Số phức giúp ta có cái nhìn hoàn toàn khác nhất là khi áp dụng vào giải các phương trình, hệ phương trình.
Nếu như trước đây, khi giải phương trình bậc 2, nếu penta lớn hơn hoặc bằng không thì phương trình sẽ có 1 nghiệm hoặc 2 nghiệm, còn nếu penta nhỏ hơn 0 phương trình đã cho sẽ vô nghiệm. Khi đó ta không cần phải giải nữa. Nhưng khi số phức ra đời, tư duy của ta sẽ cao hơn khi vì khi penta âm phương trình vẫn có nghiệm và ta phải tư duy tìm ra nghiệm đó. Vậy số phức đã ra đời như thế nào ?
Đọc thêm: Gia sư uy tín ở tphcm nói về sự ra đời của số phức
Trung tâm gia sư uy tín tphcm chia sẻ điều thú vị về số phức
Trung tâm gia sư uy tín tphcm thấy rằng số phức ra đời để mọi phương trình bậc n đều có nghiệm, việc giải phương trình sẽ trở nên thú vị hơn khi không còn trường hợp vô nghiệm như trước đây nữa. Phương trình bậc 2 thì có 2 nghiệm, phương trình bậc 3 thì có 3 nghiệm, bậc 5 thì có những 5 nghiệm, đòi hỏi người giải toán có tư duy logic cao hơn để tìm được tất cả các nghiệm của phương trình. Vậy bạn đã biết được gì về số phức ?
Bạn có biết số phức ra đời như thế nào không ? Bạn có biết số phức có những tính chất, đặc điểm gì khác với số nguyên, số thực, số hữu tỷ, số vô tỷ,…
Đọc thêm: Trung tâm gia sư uy tín tphcm chia sẻ điều thú vị về số phức
Gia sư uy tín tphcm nói về số phức
Gia sư uy tín tphcm thấy rằng toán học là một quá trình tư duy logic của con người từ thấp đến cao, từ đơn giản đến phức tạp. Bắt đầu ở cấp 1, các bạn đã được làm quen với giải phương trình tìm ra nghiệm x, tuy nhiên bài toán tìm nghiệm này khá đơn giản và kết quả x cần tìm chỉ là một số nguyên dương hoặc số nguyên âm.

Lên đến cấp 2, mức độ câu phương trình sẽ khó hơn và kết quả x cần tìm không chỉ là một số nguyên dương hay âm mà có thể là một số thực R, hoặc số hữu tỷ, vô tỷ. Đó là vì bạn được học thêm nhiều phương pháp để giải như áp dụng tam thức bậc 2 denta, sử dụng sơ đồ hoocne,… nên nghiệm x mà bạn tìm ra không đơn thuần là một số nguyên nữa.
Đọc thêm: Gia sư uy tín tphcm nói về số phức
Gia sư tại nhà nói về bất phương trình logarit
Hôm nay, Gia sư tại nhà và các bạn cùng nhau đi đến phần cuối cùng của chương II – Hàm số lũy thừa, hàm số mũ và hàm số logarit để kết thúc chương và nội dung bài học hôm nay đó là bất phương trình logarit.

Các tiết trước, chúng ta đều đã khảo sát không chỉ về hàm số logarit mà còn khảo sát về hàm số mũ, hàm lũy thừa về khái niệm, đặc trưng, tính chất, tính đơn điệu, đồ thị hàm số.
Đọc thêm: Gia sư tại nhà nói về bất phương trình logarit
- Cảm Nhận Bài Thơ Mùa Xuân Nho Nhỏ | Gia Sư Giỏi TPHCM
- Phân tích truyện ngắn lặng lẽ sa pa hay nhất | Gia sư uy tín ở TPHCM
- Cảm Nhận Bài Thơ Tiểu Đội Xe Không Kính | Tìm gia sư uy tín ở TPHCM
- Cảm nhận của em về bài thơ Đồng Chí | Gia sư uy tín TPHCM
- Gia sư tphcm tổng hợp 3 cách phòng tránh bệnh viêm phổi vũ hán hiệu quả nhất






 0908 64 0203
0908 64 0203
